-
📌 이진 검색 트리
💡 이진 검색 트리(Binary Search Trees)
- 히프의 문제점
- 임의의 데이터를 갖는 노드를 삭제할 경우의 시간 복잡도 : O(N)
- 트리에서 특정 데이터를 갖는 노드를 검색하는 시간 복잡도 : O(N)
- 이진 검색 트리란?
- 트리 내에서 특정 데이터(Key 값) 을 갖는 노드를 효율적으로 검색
- O(Log N), 하지만 정렬된 상태를 유지해야한다.
- 이진 검색 트리의 정의
- 모든 노드는 유일한 키 값을 가지고 있다.
- 왼쪽 서브 트리에 저장된 키 값 < 루트 노드의 키 값
- 오른쪽 서브 트리에 저장된 키 값 > 루트 노드의 키 값
- 양쪽 서브 트리도 이진 검색 트리이다.
💡 검색 연산
- 기본 개념
if(key == root -> data) returnif(key < root -> data) search(root -> left_child)if(key > root -> data) search(root -> right_child)- 순환 알고리즘 혹은 반복문을 이용하여 구현한다.
- 시간 복잡도는 O(트리의 Depth)
💡 이진 검색 트리에 노드 추가
- 기본 개념
- 추가할 키 값이 이미 트리에 존재하는지 확인한다.
- 트리의 유일성을 보장한다.
- 검색 알고리즘 수행 후, 알고리즘이 종료되는 곳에 새로운 노드를 추가한다.
- modified_search(root, key)
- key 가 존재할 경우,
return NULL
- 검색 알고리즘에서 방문한 마지막 노드에 대한
Pointer return
- 검색 성능은 O(Log N) 이 보장되는 것이 장점이다.
💡 이진 검색트리에서 노드 삭제
- 중위 순회를 이용하면, 오름차순으로 출력이 가능하다.
- 리프 노드 삭제
parent -> left_child = NULL

- child 가 하나밖에 없는 노드의 삭제
- 삭제된 자리에 child node 를 위치하게 한다.
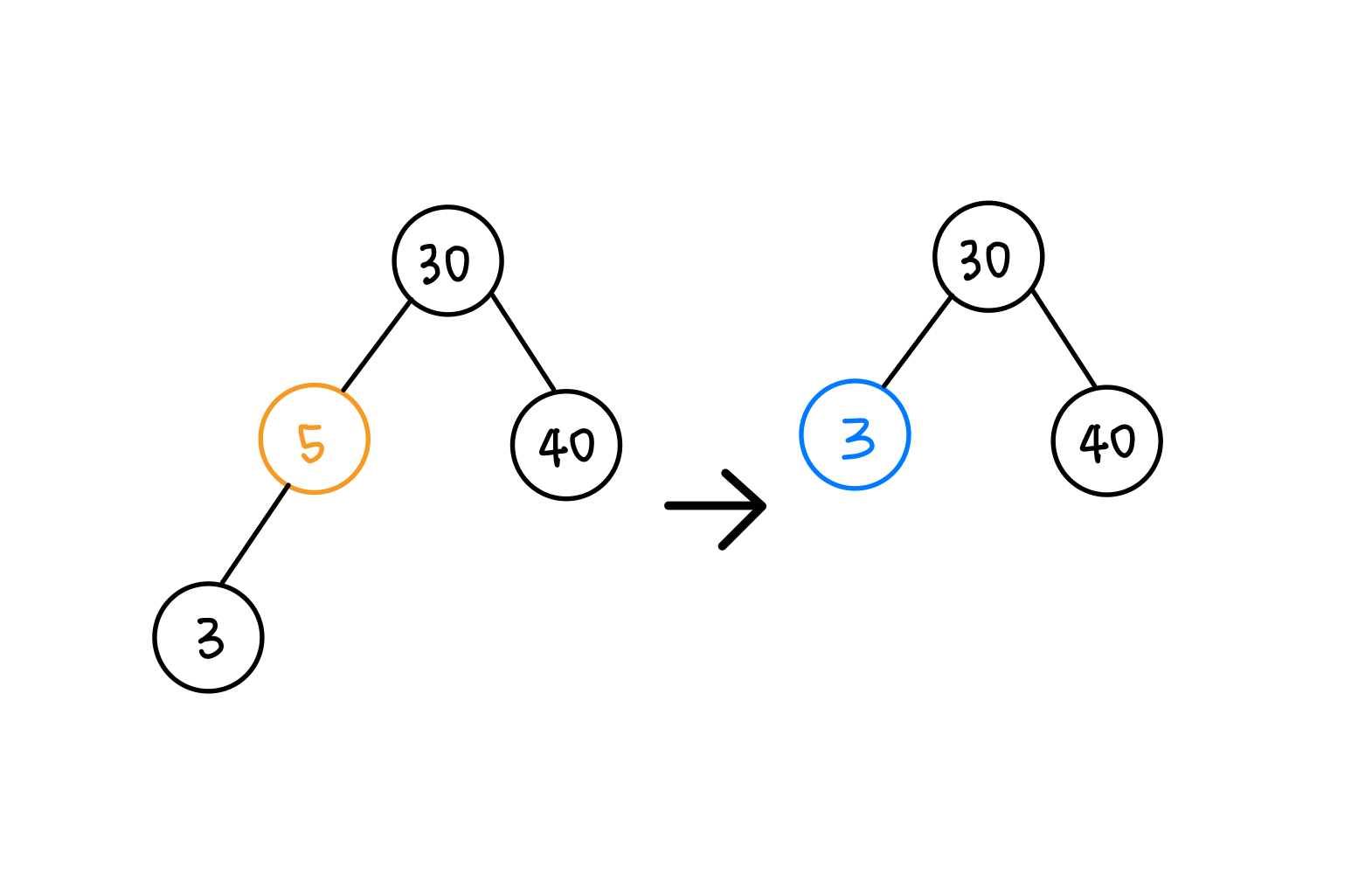
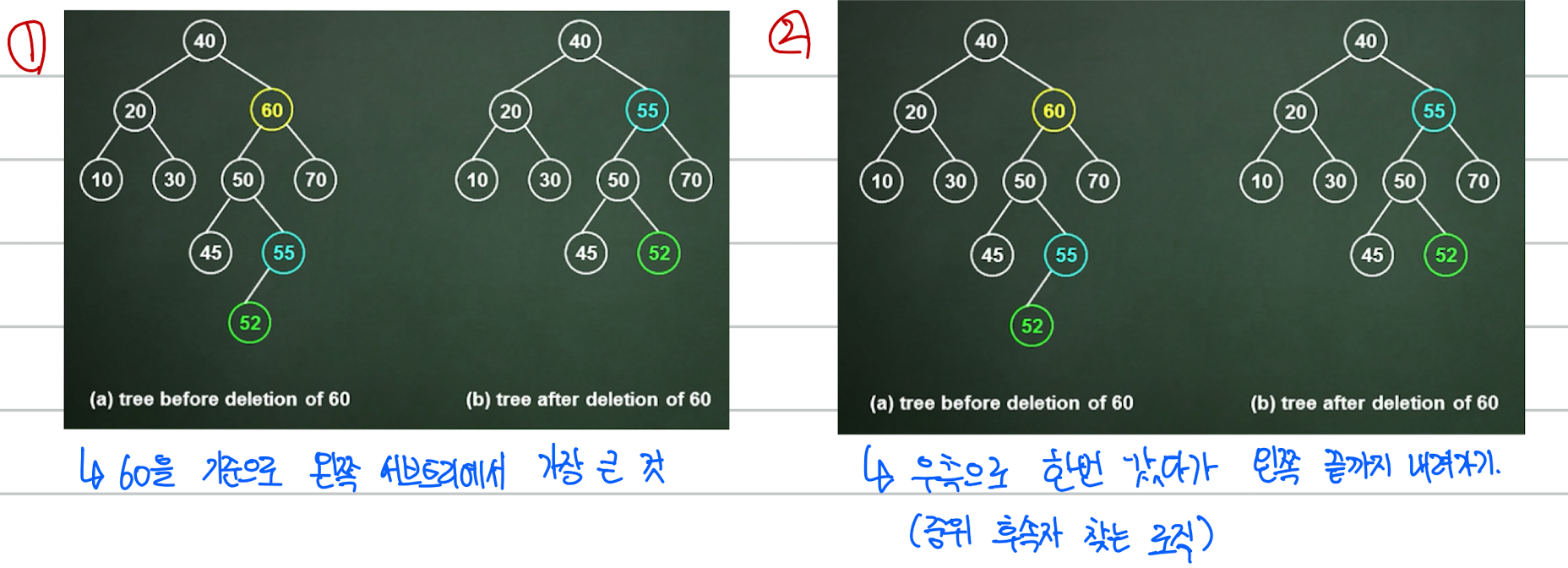
- 두개의 children 을 갖는 노드를 삭제
- 왼쪽 서브트리에서 가장 큰 노드
or
- 오른쪽 서브트리에서 가장 작은 노드를 삭제된 자리에 위치 시킨다.
💡 이진 검색 트리의 깊이
- 데이터가 정렬된 순서로 입력 : O(N)
- 1,2,3,4 : 편향 이진 트리
- 데이터가 무작위 순서로 입력 : O(Log N)
- 균형 이진 검색 트리 : AVL Tree, Red-Black Tree
- 정렬된 데이터가 들어와도 O(Log N)을 보장한다.


