트리와 이진트리의 개념

📌 트리와 이진트리의 개념

💡 트리의 개념

1. 트리란?
   1. 계층적 구조의 자료를 표현할 때 사용
   2. ex) 가계도, 회사의 조직도, 폴더 구조 등

2. 트리의 정의
   1. 하나 이상의 노드로 이루어진 유한 집합
   2. Root(루트) 라고 하는 노드가 하나 존재한다.
   3. 나머지 노드들은 n(n >= 0) 개의 집합 T[1], ... ,T[n]으로 분할
      1. 이처럼 분할된 트리를 루트의 서브트리라고 한다.

 

💡 트리에 관련된 용어들

1. Level 1 : 노드의 차수(Degree), 트리의 차(Degree)
2. Level 2 : 단일노드(Leaf node or Terminal node)
3. Level 3 : 부모노드, 자식노드, 형제노드
4. Level 4 : 조상노드, 자손노드, level, 트리의 높이 or 깊이

 

💡 이진트리의 개념

1. 이진트리(Binary Tree)란?
   1. 모든 노드의 차수가 2를 넘지 않는 트리
      1. = 일반 트리에 비해 구현이 쉽다.
   2. 왼쪽 서브트리와 오른쪽 서브트리가 구분된다.

 

 

2. 이진트리의 정의
   1. 유한한 개수의 노드들이 집합으로서 노드 수는 0이 될 수 있다.
   2. 하나의 루트노드와 왼쪽 서브트리, 그리고 오른쪽 서브트리로 구성되어있다.
   3. 각 서브트리는 다시 이진트리이다.

3. 트리를 이진트리로 변환하는 방법
   1. Left child - Right sibling 표현
      1. 노드 A의 제일 왼쪽 노드 : A의 왼쪽 자식 노드
      2. A의 나머지 자식 노드들 : 자식 노드의 오른쪽 노드

 

💡 이진트리의 성질

1. 최대 노드 수
   1. 이진 트리의 레벨 i 에서 최대 노드 수는 2^(i-1) (i > 0)
   2. 깊이가 k인 이진트리가 가질 수 있는 최대 노드 수

 

2. 단말 노드 수와 차수가 2인 노드 수
   1. N[0] : 단말 노드수
   2. N[2] : 차수가 2인 노드의 수 = N[0] = N[2] + 1

3. 정의 : 깊이가 K인 포화 이진트리(Full Binary Tree)
   1. 깊이가 K 이고, 노드 수가 2 ** (k >= 0) 인 이진트리

💡 완전이진트리(Complete Binary Tree)

1. 완전이진트리란?
   1. 깊이가 K이고 노드 수가 N 인 이진트리의 각 노드들이 깊이가 K인 포화이진트리에서 1부터 N까지의 번호를 붙인 노드들과 1대1로 일치하는 이진트리.
   2. 마지막 레벨을 제외하고 포화이진트리이며, 마지막 레벨에서 왼쪽부터 빠짐없이 노드가 채워진 형태로 트리가 구성된 경우를 말한다.

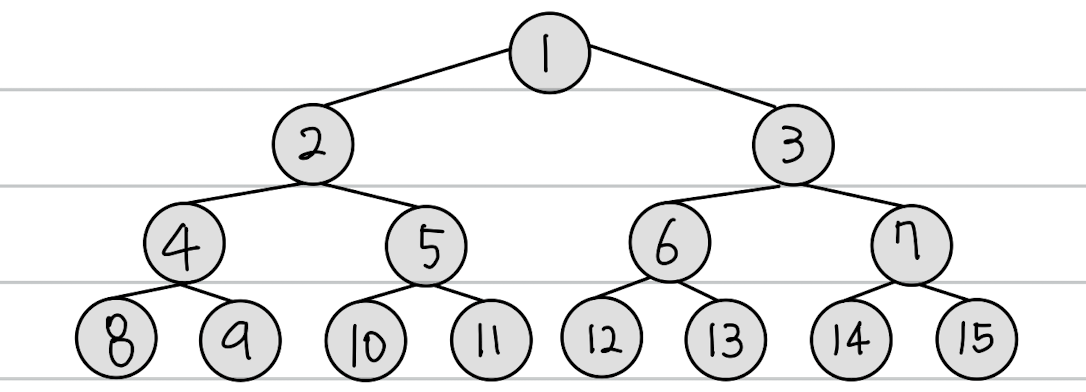
💡 이진트리의 표현

1. 배열 표현법 - 1차원 배열에 저장 (완전이진트리 저장에 적합)
   1. 루트 노드는 [1] 에 저장한다.
   2. 부모 노드가 [i] 에 저장될 경우
      1. 왼쪽 자식 노드는 [i * 2]에 저장한다.
      2. 오른쪽 자식 노드는 [i * 2 + 1]에 저장한다.
      3. 이 때, i 번째 노드의 부모 인덱스는 i // 2 이다.
   3. 만약 2의 제곱수에 해당하는 인덱스에만 데이터가 들어가있다면, 그 트리는 편향 이진트리이다.

2. 링크 표현법
   1. 노드를 구조체로 표현 
   2. * 코드
   3. stuct node{ char data; struct node *left_child; strcut node *right_child; };
   4. 노드의 수가 N 일 경우, 링크의 수 = 2N
   5. NULL 인 link 의 수는 N + 1